5f+1 orbital

8. One-Electron Atoms#

Just as the touchstone of chemistry is the periodic table, the touchstone of quantum chemistry is the atomic wavefunction. As we shall see, our intuition about many-electron atoms is built up from our knowledge of 1-electron atoms, mainly because many-electron atoms are mathematically intractable, while 1-electron atoms are not appreciably more complicated than an electron confined to a spherical ball. A detailed mathematical exposition on 1-electron atoms–which are often called hydrogenic atoms–is provided as a pdf. This is only a brief summary.

Schrödinger Equation for One-Electron Atoms#

Denoting the mass of the electron as \(m_e\), the charge of the electron as \(=e\), and the permittivity of free space as \(\epsilon_0\), the Hamiltonian for the attraction of an electron to a atomic nucleus with atomic number \(Z\) (and charge \(+Ze\)) at the origin, \((x,y,z) = (0,0,0)\), is:

\[ \hat{H}_{\text{1 el. atom}} = -\frac{\hbar^2}{2m_e} \nabla^2 - \frac{Z e^2}{4 \pi \epsilon_0 r} \]

where \(r = \sqrt{x^2+y^2+z^2}\) is the distance of the electron from the nucleus. In atomic units, the Hamiltonian is:

\[ \hat{H}_{\text{1 el. atom}} = -\tfrac{1}{2} \nabla^2 - Zr^{-1} \]

Just as we did for the electron confined to a spherical ball, we rewrite the Schrödinger equation in spherical coordinates,

\[ \left(-\frac{1}{2} \left( \frac{d^2}{dr^2} + \frac{2}{r} \frac{d}{dr}\right) + \frac{\hat{L}^2}{2r^2} - \frac{Z}{r} \right) \psi_{n,l,m_l}(r,\theta,\phi) = E_{n,l,m_l}\psi_{n,l,m_l}(r,\theta,\phi) \]

and use the fact the eigenvalues of the squared-magnitude of the angular momentum, \(\hat{L}^2\) are the spherical harmonics

\[ \hat{L}^2 Y_l^{m} (\theta, \phi) = l(l+1)Y_l^{m} (\theta, \phi) \qquad l=0,1,2,\ldots m=0, \pm 1, \ldots, \pm l \]

and the technique of separation of variables to deduce that the wavefunctions of one-electron atoms have the form

\[ \psi_{n,l,m}(r,\theta,\phi) = R_{n,l}(r) Y_l^{m}(\theta,\phi) \]

where the radial wavefunction, \(R_{n,l}(r)\) is obtained by solving the radial Schrödinger equation

\[ \left(-\frac{1}{2} \left( \frac{d^2}{dr^2} + \frac{2}{r} \frac{d}{dr}\right) + \frac{l(l+1)}{2r^2} - \frac{Z}{r} \right) R_{n,l}(r) = E_{n,l}R_{n,l}(r) \]

The Radial Equation for One-Electron Atoms#

To solve the radial Schrödinger equation, we rewrite it as a homogeneous linear differential equation

\[ \left( \frac{d^2}{dr^2} + \frac{2}{r} \frac{d}{dr} - \frac{l(l+1)}{r^2} + \frac{2Z}{r} + 2E_{n,l}\right) R_{n,l}(r) = 0 \]

It is (quite a bit) more involved than the previous cases we have considered, but the same basic technique reveals that the eigenenergies are

\[ E_n = -\frac{Z^2}{2n^2} \]

and the radial wavefunctions are the product of an associated Laguerre polynomial and an exponential,

\[ R_{n,l}(r) \propto \left(\frac{2Zr}{n}\right)^l L_{n-1-l}^{2l+1}\left(\frac{2Zr}{n}\right) e^{-\frac{Zr}{n}} \]

with

\[\begin{split} n=1,2,3,\ldots \\ l=0,1,\ldots,n-1 \\ m = 0,\pm 1, \pm2, \ldots, \pm l \end{split}\]

Hydrogenic orbitals

Eigenenergies and Wavefunctions for One-Electron Atoms#

The eigenenergies of the Hydrogenic wavefunctions do not depend on \(m\) or \(l\). So there are \((n+1)^2\) degenerate eigenfunctions, with energies

\[ E_n = -\frac{Z^2}{2n^2} \]

The energy eigenfunctions are:

\[ \psi_{nlm}(r,\theta,\phi) \propto \left(\frac{2Zr}{n}\right)^l L_{n-1-l}^{2l+1}\left(\frac{2Zr}{n}\right) e^{-\frac{Zr}{n}} Y_l^{m} (\theta, \phi) \]

These eigenfunctions are complex-valued, because the spherical harmonics are complex-valued. Like all other one-electron wavefunctions, these eigenfunctions are referred to as orbitals. For historical reasons, orbitals are labelled by their principle quantum number \(n\) (which specifies their energy), their total angular momentum quantum number \(l\), and the quantum number that specifies their angular momentum around the \(z\) axis, \(m\),

\[ \hat{L}_z Y_l^{m} (\theta, \phi) = \hbar m Y_l^{m} (\theta, \phi) \]

The \(l\) quantum number is stored by a letter code that dates back to the pre-history of quantum mechanics, where certain spectral lines were labelled as sharp (\(l=0\) indicated no spatial degeneracy that could be broken by an external field), principle (\(l=1\) lines were still relatively sharp), diffuse (\(l=2\) lines were quite diffuse due to the 5-fold degeneracy of d orbitals), and fundamental (\(l=3\)).

Note that the orbital images that appear above do not look that much like the usual orbital pictures, with the exception of the \(m=0\) orbitals. This is because of the complex-valuedness. We often instead use the real spherical harmonics, which are defined simply as:

\[\begin{split} \begin{align} S_l^{m>0}(\theta,\phi) &= \frac{1}{\sqrt{2}} \left(Y_l^{-m} (\theta, \phi) + (-1)^{m} Y_l^{m} (\theta, \phi) \right) \\ S_l^{m=0}(\theta,\phi) &= Y_l^{m=0} (\theta, \phi) \\ S_l^{m<0}(\theta,\phi) &= \frac{i}{\sqrt{2}} \left(Y_l^{-m} (\theta, \phi) - (-1)^{m} Y_l^{m} (\theta, \phi) \right) \end{align} \end{split}\]

The following animations shows one can take linear combinations of the (complex) spherical harmonics to form the \(p_x\), \(p_y\), etc. orbitals one generally uses in chemistry.

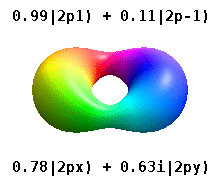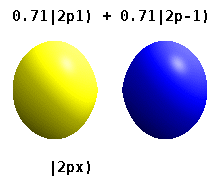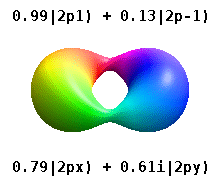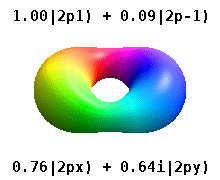
animation of 2p orbital

animation of 3p orbital

Using the orbitron, you can visualize the (real, Cartesian) spherical harmonics and the radial wavefunctions for hydrogenic orbitals. Most orbitals have very complicated formulas, but a few have simple equations, including:

\[\begin{split} \psi_{\text{1s}}(r) = \psi_{100}(r) = \sqrt{\frac{Z^3}{\pi}}e^{-Zr} \\ \psi_{n,n-1,m} \propto r^{n-1} e^{\tfrac{-Zr}{n}} Y_l^{m_l} (\theta,\phi) \end{split}\]

📝 What is the expectation value of \(r^k\) for the \(l=n-1\) orbital of a hydrogenic atom.#

📝 Show that the energy of the Hydrogen atom in arbitrary units (not necessarily atomic units) can be written as:#

\[ E_n = -\frac{Z^2}{2n^2} \cdot \left(\frac{e^2}{4 \pi \epsilon_0}\right)^2 \cdot \left( \frac{m_e}{\hbar^2}\right) \]

🪞 Self-Reflection#

  • Using the conversion from atomic units to traditional chemical units of kJ/mol, what is the energy of the Hydrogen atom? How accurately, in atomic units, must one determine the energy of a one-electron atom in order to attain “chemical accuracy” of ~1 kJ/mol?

  • Write a small Python script to evaluate the expectation value of the radius, \(r\), for a one-electron atom.

  • Test to confirm that the Heisenberg uncertainty principle for position and momentum holds for the ground state of a Hydrogenic atom.

  • To what extent is the shape of the spherical harmonic intuitive, especially the doughnut shapes associated with an electron’s angular momentum around the z axis.

🤔 Thought-Provoking Questions#

  • In one-electron atoms, the eigenenergies depend only on the principle quantum number, \(n\), and not the angular momentum quantum number, \(l\). Why are \(s\) orbitals lower in energy than \(p\) orbitals in real multielectron atoms, but not one-electron atoms? It turns out this is not an accidental degeneracy, but a hidden symmetry of the Hydrogen atom.

  • Suppose electrons did not repel each other. Can you write the wavefunction for a many-electron atom in that case?

  • Why do you think solving the Schrödinger equation for the one-electron molecule is more complicated than solving the Schrödinger equation for the one-electron atom?

  • For what \(Z\) is the energy of a one-electron atom comparable to the rest-mass energy of an electron, \(mc^2\)? For atomic numbers close to this value, relativistic effects become extremely important.

  • The Kratzer-Fues potential, \(V_{\text{Kratzer-Fues}}(r) = \frac{a}{r^2} - \frac{b}{r}\) (here \(a>0\) and \(b>0\)) is a reasonable model for a diatomic molecule rotating and vibrating in 3 dimensions, or even a ion-pair complex (e.g., an single ion pair from an ionic solvent in the gas phase). What are the solutions to the Schrödinger equation for the Kratzer-Fues potential? Solution

\[ \left(-\frac{\hbar^2}{2m}\nabla^2 +\frac{a}{r^2} - \frac{b}{r} \right) \psi(\mathbf{r}) = E\psi(\mathbf{r}) \]

🔁 Recapitulation#

  • What are eigenfunctions for the \(n=l+1\) state of a one-electron atom?

  • What are the energy eigenfunctions and eigenvalues for a one-electron atom?

  • How does the energy increase as the atomic number increases?

🔮 Next Up…#

  • Multielectron systems

  • Approximate methods.

📚 References#

My favorite sources for this material are:

There are also some excellent wikipedia articles: